September 2020

Fungsi

Fungsi atau pemetaan sering kita temukan dalam kehidupan sehari-hari. Fungsi merupakan relasi khusus atau hubungan khusus antara suatu himpunan dengan himpunan yang lain. Misalnya hubungan anak dengan ibu kandung. Semua anak di dunia ini memiliki ibu kandung dan hanya memiliki satu ibu kandung. ya... itulah relasi atau hubungan antara anak dengan ibu kandung merupakan salah satu contoh fungsi yang dapat kita temukan dalam kehidupan sehari-hari.

Contoh lain dari penerapan fungsi adalah penggunaan sandi. Bagi anak pramuka pasti bukan hal asing ya menggunakan sandi. Ternyata sandi menggunakan konsep matematika lho... khususnya bab mengenai relasi dan fungsi. Coba perhatikan gambar di bawah ini.

Gambar di atas merupakan sebuah pesan. Kita harus mengetahui kode sandi dari pesan tersebut agar bisa membacanya. Sekarang coba perhatikan kode sandi untuk pesan di atas.

Setelah melihat kode sandi di atas dapatkah kalian membaca pesan tersebut? Coba kalian tuliskan di kolom komentar isi dari pesan di atas.

Manfaat fungsi sangat banyak sekali baik dalam bidang tekonologi, kesehatan, dan lain sebagainya. Sehingga sangat penting untuk kita pelajari.

1. Pengertian fungsi

Fungsi dari dari himpunan A ke himpunan B merupakan relasi khusus yang memasangkan setiap anggota himpunan A dengan tepat satu ke anggota himpunan B. Dari pengertian tersebut perlu kita garis bawahi kata setiap dan tepat satu. Setiap artinya semua anggota himpunan A memiliki pasangan di B. Kemudian tepat satu artinya anggota himpunan A memiliki pasangan hanya ada satu di anggota himpunan B, tidak boleh lebih lebih dari satu. Jadi dapat kita tarik kesimpulan syarat suatu relasi dapat dikatakan fungsi adalah:

a. Setiap anggota himpunan A mempunyai pasangan di himpunan B

b. Setiap anggota himpunan A dipasangkan dengan tepat satu anggota himpunan B.

Jika kedua syarat tersebut terpenuhi maka relasi tersebut adalah fungsi.

Example:

1. Fungsi karena kedua syarat terpenuhi.

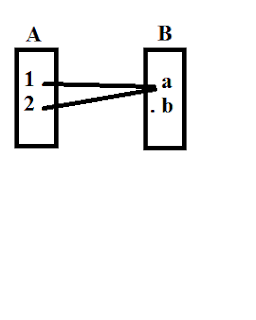
2. Bukan fungsi karena ada anggota A yang memiliki pasangan lebih dari satu. Anggota A yaitu 2 memiliki pasangan a dan c, sehingga contoh di bawah ini bukan fungsi karena syarat ke-2 tidak terpenuhi

3. Bukan fungsi karena syarat ke-1 tidak terpenuhi. Ada anggota A yang tidak memiliki pasangan di B yaitu 3.

4. Fungsi karena kedua syarat terpenuhi

2. Notasi fungsi

Notasi fungsi biasanya disimbolkan dengan huruf kecil. Suatu fungsi f yang memetakan x anggota himpunan A ke y anggota himpunan B dapat dinotasikan sebagai berikut.

f:xà y atau f:x à f(x)

Dibaca: fungsi f memetakan x anggota A ke y anggota B

3. Domain, kodomain, dan Range

Perhatikan fungsi yang disajikan dalam bentuk diagram panah di bawah ini:

A={1, 2, 3} disebut daerah asal atau domain

B={a, b, c, d, e} disebut daerah kawan atau kodomain

R={a, c, e} disebut daerah hasil atau range.

Daerah hasil merupakan himpunan dari anggota-amggota kodomain yang mempunyai pasangan dengan anggota domain.

4. Menentukan banyaknya fungsi atau pemetaan yang mungkin dari dua himpunan

Misalkan diketahui himpunan A={1,2} memiliki dua anggota atau n(A)=2 dan himpunan B={a,b} yang memiliki dua anggota atau n(B)=2. Banyaknya pemetaan atau fungsi dari A ke B adalah sebagai berikut:

Ternyata banyaknya pemetaan dari A ke B adalah 4.

Pertanyaanya, bagaimana jika A memiliki 4 anggota dan B memiliki 5 anggota? Akankah kita membuat pemataan seperti contoh di atas? Bisa, tetapi pasti membutuhkan waktu yang lama. Maka dari itu kita membutuhkan rumus tertentu untuk menentukan banyaknya pemetaan yang mungkin dari A ke B atau sebaliknya.

Jika banyak anggota himpunan A adalah n(A) dan banyak anggota himpunan B adalah n(B):

a. Banyak pemetaan yang mungkin dari A ke B adalah

, dan

b. Banyak pemetaan yang mungkin dari B ke A adalah

Example :

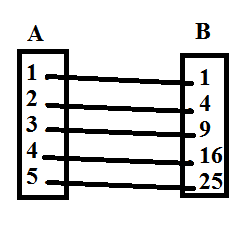
Diketahui A={1,2,3,4} dan B={a,b,c,d,e}. Tentukan banyaknya pemetaan dari A ke B.

n(A)= 4 dan n(B)= 5

maka banyaknya pemetaan dari A ke B adalah

Jadi banyaknya pemetaan yang mungkin dari A ke B adalah 625. Wah cukup banyak juga ya... bayangkan jika kalian mencarinya menggunakan diagram panah. (pasti butuh waktu ya...)

latihan!

1. Manakah yang merupakan fungsi?